집합 알고리즘에 주로 사용되는 연산: 합치기, 탐색
Union: 합치기, Find: 탐색
활용 시나리오
- 조건: 여러 개의 그룹이 형성되어 있음
- 문제: 특정 원소가 주어졌을 때, 이 원소들이 같은 그룹인지 판단해야 할 경우
유니온-파인드 알고리즘과 경로 압축 알고리즘 활용
파인드 연산
특정 노드의 루트 노드가 무엇인지 탐색하는 방법
- 특정 노드가 같은 집합에 있는지 확인할 때 사용
A, B 두 노드가 있을 때 이 노드의 루트 노드가 서로 같다면 같은 집합에 속한 것
특정 노드부터 재귀로 거슬러 올라가며 루트 노드를 찾음
과정
- 현재 노드의 부모 노드를 확인한다. 부모 노드를 확인하다가 부모 노드가 루트 노드이면 찾기 연산을 종료한다.
- 1에서 찾기 연산이 종료되지 않으면 1을 반복한다.
1단계
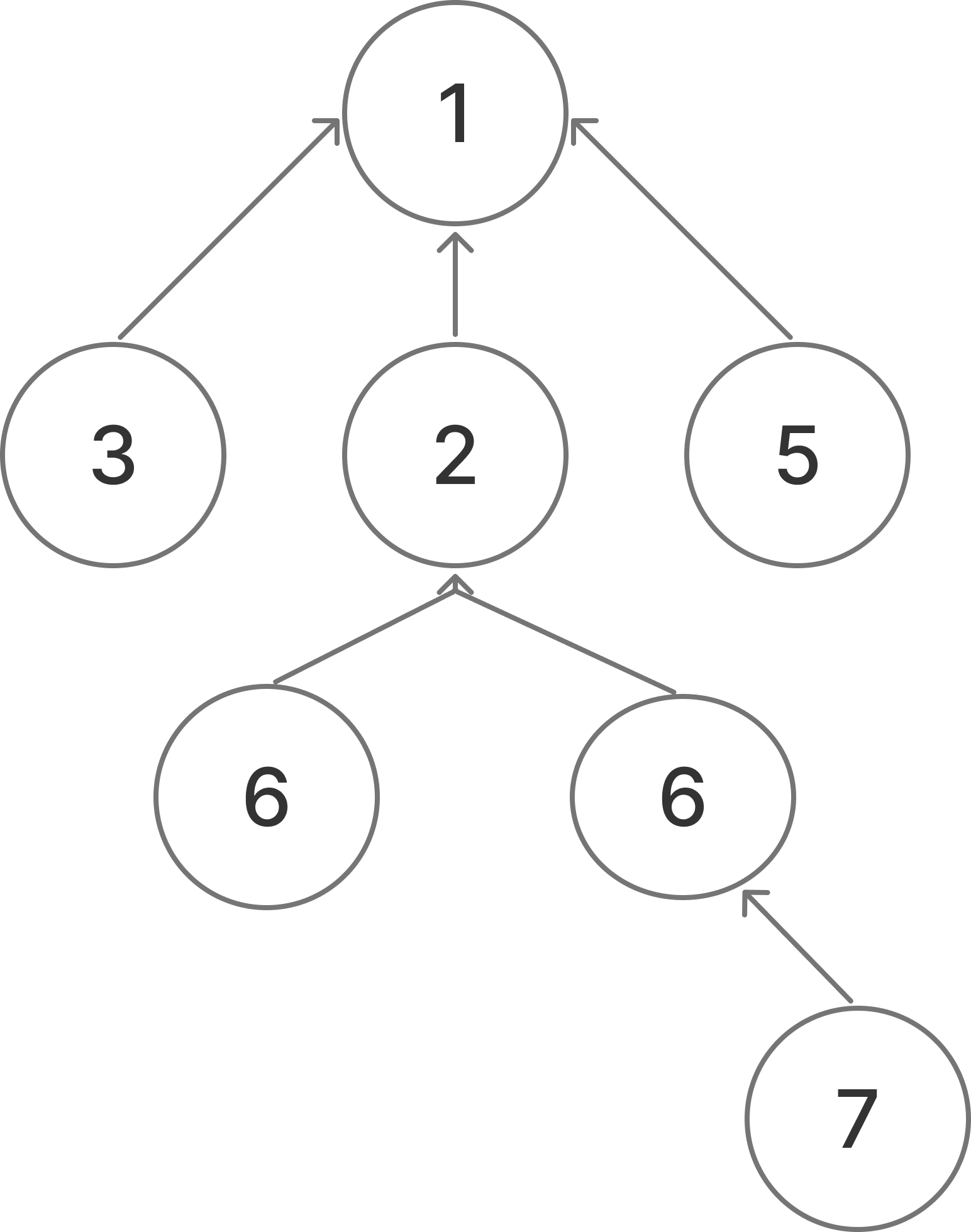
집합을 정의하고, 노드 7의 루트 노드를 찾는 과정을 살펴보자.
→ find(7)

2단계
노드 7의 루트 노드를 찾는다.
현재 노드와 부모 노드가 같을 때까지 탐색한다.
노드 7 → 6 → 2 → 1
- 현재 노드를 1가 1인 경우, 노드 1의 부모 노드는 1이다
따라서, 현재 노드와 부모 노드가 같으므로 루트 노드 1을 찾을 수 있다.
이와 같이 탐색 연산은 재귀 함수로 구현한다.
→ 루트 노드를 현재 노드와 부모 노드가 같을 때까지 진행해서 최종 값 반환
유의사항 최악의 경우 시간 복잡도: O(N)
예시
find(4) 실행할 경우, 모든 노드를 거쳐야 루트 노드를 찾을 수 있다.


파인드 연산에서 목표로 하는 것은 ‘루트 노드 찾기’ 이므로, 매번 모든 부모 노드를 탐색하는 과정은 비효율적이다.
→ 한 번 find(4) 를 수행해서 결과가 1인 것을 알았다면, 노드 2, 3, 4는 루트 노드가 아님이 명확해서 다시 수행할 경우 노드 2, 3을 다시 확인할 필요가 없다.
파인드 연산의 연산 비용 문제 해결: 경로 압축
집합 형태를 유지하면서 트리 높이를 줄이면 된다.
→ 트리의 높이를 줄이므로 부모 노드를 거치는 과정을 줄일 수 있다.
→ 최악의 경우 수행해야 할 연산 횟수가 줄어든다.

- find(2), find(3), find(4) 연산이 모두 한 번에 수행될 수 있다.
합치기 연산
두 집합을 하나로 합치는 연산
→ 두 집합의 루트 노드를 동일하게 하는 것
루트 노드는 두 집합의 루트 노드 중 하나가 되면 된다.
과정
- 주어진 두 노드의 루트 노드를 찾기 연산을 통해 찾는다.
- 각 노드가 속한 집합을 합친다. → 두 집합의 루트 노드를 같게 한다. → 루트 노드는 두 집합 중 어떤 루트 노드로 해도 상관 없다. → 만약 이미 두 집합의 루트 노드가 동일하다면 같은 집합에 속해있는 것이다.
1단계
집합 A = {1, 3, 5}, 집합 B = {2, 7, 9}

2단계
집합 A, B의 리프 노드 중 임의의 노드 5와 7의 루트 노드를 찾는다고 가정한다.
찾기 연산을 수행하면 노드 5 → 1, 노드 7 → 2 다.
3단계
루트 노드가 2인 집합의 루트 노드를 1로 변경한다.

4단계
두 집합이 잘 합쳐졌는지 검증
- 집합 A 의 변경사항은 없다.
- 집합 B 는 루트 노드의 부모 노드가 2 → 1 로 변경되었다.
- 노드 9에서 부모 노드를 쫓아가면 루트 노드가 1이 나온다. → OK!
유니온 연산의 연산 비용 문제 해결: 랭크
파인드 연산과 마찬가지로 트리의 깊이가 깊어질 수록 연산 비용이 커진다.
이를 개선하기 위해 랭크 기반 유니온-파인드 알고리즘을 사용할 수 있다.
→ 도입 목적: 트리 균형 유지하기
유니온-파인드 알고리즘 기업 입사 코딩 테스트에 출제 되기에는 난이도가 높은 편이라고 함.
랭크
현재 노드를 기준으로 하였을 때 가장 깊은 노드까지의 경로 길이를 말한다.
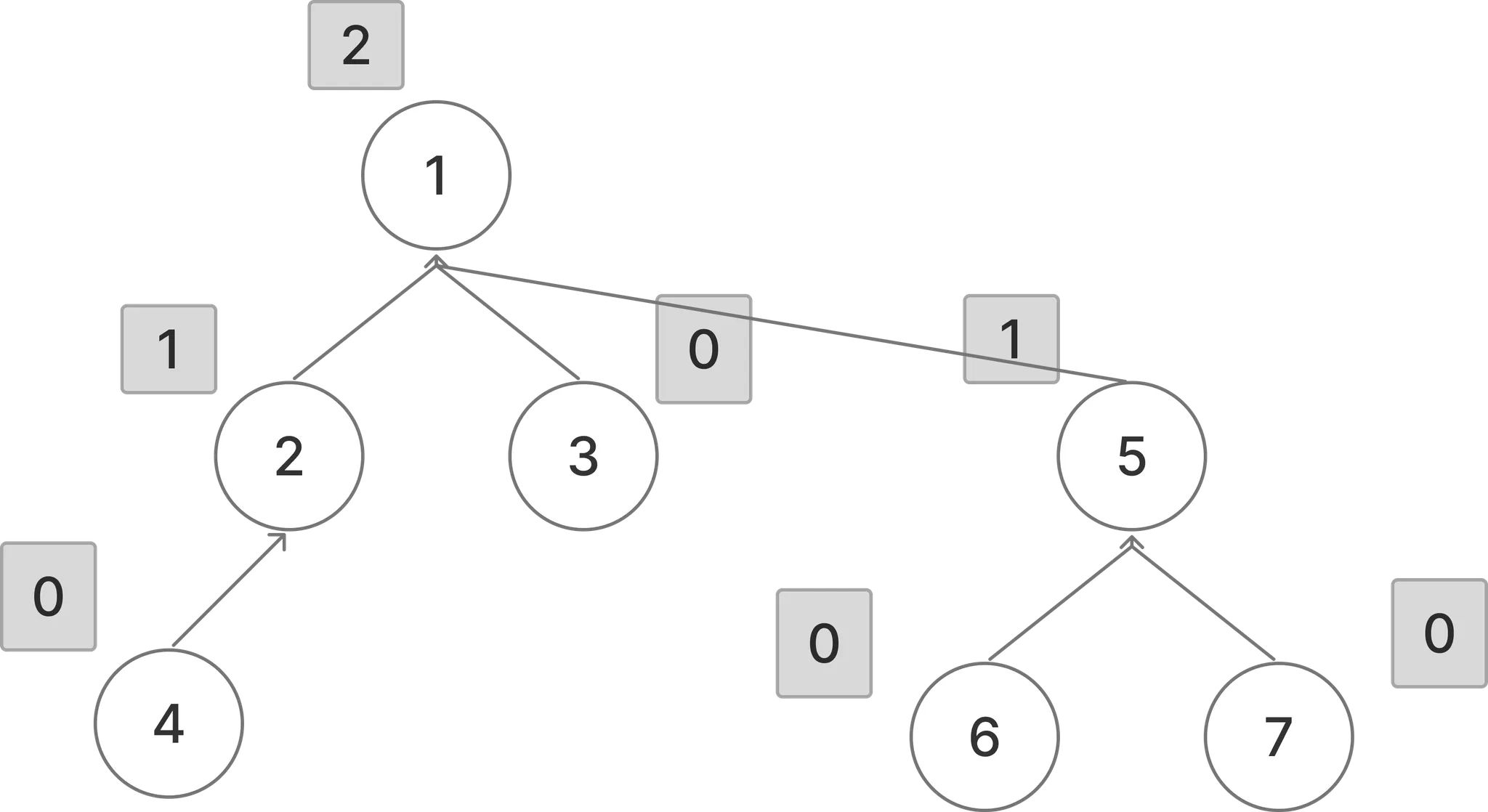
각 노드에 랭크를 표시하면 이와 같다.
- 1 → 노드 4까지의 경로가 가장 깊기 때문에 2
- 4, 3 → 해당 노드보다 더 깊은 노드가 없으므로 0
- 2 → 노드 4보다 1 깊음

- 두 노드의 루트 노드를 구한다.
- 1에서 구한 루트 노드의 랭크를 비교한다.
- 랭크 값이 다르면 랭크 값이 큰 루트 노드를 기준으로 삼는다. → 랭크가 더 큰 루트 노드를 랭크가 작은 루트 노드의 부모 노드로 바꾼다. → 트리의 깊이는 더 깊어지지 않으므로 랭크의 값은 변하지 않는다.
- 랭크 값이 같으면 루트 노드를 아무거나 선택해서 바꾸고 최종 루트 노드의 랭크에 1을 더한다.
1단계
집합 2개 정의

2단계
두 집합을 랭크 기반으로 합친다.
노드 1 랭크 → 2, 노드 5 랭크 → 1
→ 노드 1의 랭크가 더 크므로 노드 5의 부모 노드를 1로 변경한다.
노드 1의 랭크를 바꿀 필요가 없다.
→ 집합의 랭크 값을 바꾼다는 것은 트리의 깊이가 깊어진다는 것을 의미하는데, 최소 1만큼 크므로 트리가 깊어지지 않는다.
'Develop > Coding Test | Algorithm' 카테고리의 다른 글
| DFS BFS 프루닝 기법 (0) | 2025.05.22 |
|---|---|
| 벨만-포드 알고리즘 (0) | 2025.04.25 |
| 원형 큐 (0) | 2025.02.14 |
| Tree 전위, 중위, 후위 순회 (1) | 2024.11.07 |
| 알고리즘 정리 및 예제 (1) | 2024.10.22 |


댓글