그래프 최단 경로 구하기 2. 벨만-포드 알고리즘
최단 경로는 '가중치' 유무에 따라 다르다
가중치가 없는 그래프에서는 간선 개수가 가장 적은 경로
가중치가 있는 그래프에서는 가중치의 총합이 최소가 되는 경로
벨만-포드 알고리즘
노드에서 노드까지의 최소 비용을 구한다.
매 단계마다 모든 간선의 가중치를 다시 확인하여 최소 비용을 갱신하므로, '음의 가중치'를 가지는 그래프에서도 최단 경로를 구할 수 있는 특징이 있다.
다익스트라 알고리즘은 음의 가중치를 허용하지 않는다는 점과 차별화된다.
- 시작 노드 최소 비용:0, 나머지 노드 INF 초기화 (최소 비용을 갱신할 때 직전 노드 갱신)
- 노드 개수 -1 만큼 연산 반복
- 최소 비용보다 더 적은 최소 비용이 있는지 확인하여 갱신하고, 직전 노드 값도 같이 갱신한다.
- 마지막에 과정 2번을 한 번 더 수행해서 갱신되는 최소 비용이 있는지 확인, 있다면 음의 순환이 있다는 것을 의미함
예시
시작 노드를 A 로 정하고 최소 비용을 0, 직전 노드를 A, 나머지 노드는 INF 로 초기화한다.
간선이 없는 경우 INF 로 계산
해당 정점의 최소 비용: 최소_비용(A)(숫자)
가중치가 있는 간선: 간선(A, B)(숫자)

A 에서 시작하는 경우
- 최소_비용(A)(0) == 최소_비용(A)(0) + 간선(A, A)(0): 갱신하지 않음
- 최소_비용(B)(INF) > 최소_비용(A)(0) + 간선(A, B)(4) : 최소_비용(B) INF -> 4
- 최소_비용(C)(INF) > 최소_비용(A)(0) + 간선(A, C)(3) : 최소_비용(C) INF -> 3
- 최소_비용(D)(INF) == 최소_비용(A)(0) + 간선(A, D)(INF): 갱신하지 않음
- 최소_비용(E)(INF) > 최소_비용(A)(0) + 간선(A, E)(-6) : 최소_비용(E) INF -> -6

A -> B -> 다음 노드로 이동하는 경우
- 최소_비용(A)(0) < 최소_비용(B)(4) + 간선(B, A)(INF) : 갱신하지 않음
- 최소_비용(B)(4) == 최소_비용(B)(4) + 간선(B, B)(0) : 갱신하지 않음
- 최소_비용(C)(3) < 최소_비용(B)(4) + 간선(B, C)(INF) : 갱신하지 않음
- 최소_비용(D)(INF) > 최소_비용(B)(4) + 간선(B, D)(5) : 최소_비용(D) INF -> 9
- 최소_비용(E)(-6) < 최소_비용(B)(4) + 간선(B, E)(INF) : 갱신하지 않음
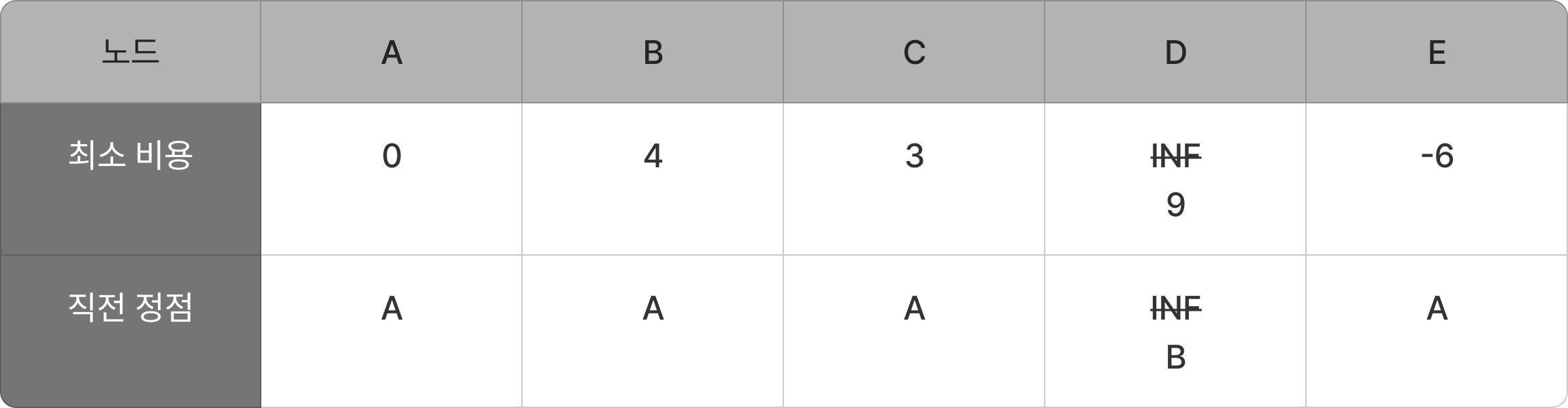
A -> C -> 다음 노드로 이동하는 경우
- 최소_비용(A)(0) < 최소_비용(C)(3) + 간선(C, A)(INF) : 갱신하지 않음
- 최소_비용(B)(4) < 최소_비용(C)(3) + 간선(C, B)(2) : 갱신하지 않음
- 최소_비용(C)(3) == 최소_비용(C)(3) + 간선(C, C)(0) : 갱신하지 않음
- 최소_비용(D)(9) < 최소_비용(C)(3) + 간선(C, D)(INF) : 갱신하지 않음
- 최소_비용(E)(-6) < 최소_비용(C)(3) + 간선(C, E)(INF) : 갱신하지 않음
A -> D 방법은 없음
A -> E -> 다음 노드로 이동하는 경우
- 최소_비용(A)(0) < 최소_비용(E)(-6) + 간선(E, A)(INF) : 갱신하지 않음
- 최소_비용(B)(4) < 최소_비용(E)(-6) + 간선(E, B)(2) : 갱신하지 않음
- 최소_비용(C)(3) > 최소_비용(E)(-6) + 간선(E, C)(2) : 최소_비용(C) 3 -> -4
- 최소_비용(D)(9) < 최소_비용(E)(-6) + 간선(E, D)(INF) : 갱신하지 않음
- 최소_비용(E)(-6) < 최소_비용(E)(-6) + 간선(E, E)(INF) : 갱신하지 않음

첫 번째 반복 종료
이 과정을 노드 개수 - 1 번 반복한다.
정점 개수 - 1 만큼 반복하는 이유는? 매 연산마다 최단 경로 1개씩 확정되기 때문이다.
-> 최단 경로에 포함될 수 있는 간선의 최대 수가 V - 1 개이다.
시작 노드가 1일 때 최단 경로를 구하는 상황인 경우, 연산을 K번 반복하면 K개의 간선에 대한 최단 경로를 구할 수 있다.

최단 경로: 같은 정점을 두 번 이상 방문하지 않는 경로 (사이클이 없는 경로)
- 정점이 V 개인 경우: 사이클이 없는 경로에서 방문할 수 있는 최대 정점 수는 V개
- 따라서 포함될 수 있는 간선은 최대 V - 1개
정점: A → B → C → D
정점 수 V = 4 → 최대 간선 수 = 3 = V - 1만약, V -1 번 후에도 거리 갱신이 일어나면 사이클이 있다는 뜻이고, 특히 음수 가중치의 사이클이라면 무한히 줄어드는 거리가 가능하므로 오류가 발생한다!
그래서 추가로 한 번 더 반복해서 음수 사이클이 있는지 확인해야 한다.
한계점
- 시간 복잡도가 느리다 O(V * E)
- 각 간선에 대해 V - 1번 반복하기 때문에, 대규모 그래프에서 비효율적이다
- 다익스트라 알고리즘 O(E + VlogV) 에 비해 매우 느린 편
- 예시) 1,000 개 정점과 500,000 간선 -> 499,000,000번 연산
- 실제 응용에서 활용 범위가 제한적
- 음의 가중치가 있는 그래프여서 음수 가중치나 음수 사이클 탐지에만 사용됨
- 대부분의 문제는 다익스트라 알고리즘으로 더 빠르게 해결 가능
- 음수 사이클이 있는 경우 경로가 무의미
- 계속해서 사이클을 돌면 -∞ 가능
- 경로 자체를 출력하거나 추적하기 어려움
- 병렬 처리 어려움
- 각 반복에서 이전 상태에 기반하여 갱신돼서 동시에 업데이트하기 쉽지 않음
- 반면, 다익스트라는 우선순위 큐 기반이라 병렬 최적화에 유리
보완 방법
- SPFA (Shortest Path Faster Algorithm): 벨만-포드를 개선한 알고리즘, 평균적으로 훨씬 빠름
- Johnson’s Algorithm: 모든 쌍 최단 경로 문제에서 음수 가중치가 있어도 해결 가능
왜 벨만-포드를 배우는가?
1. 음수 가중치와 음수 사이클을 다루는 유일한 기본 알고리즘
- 다익스트라는 음수 가중치에서 실패함
- 벨만-포드는 유일하게 음수 사이클까지 탐지 가능
- 이는 금융 거래, 환율 변환, 게임 맵 계산 등 특수한 상황에서 중요
예시) 환율 그래프에서 음수 사이클이 생기면 → 무한 수익(Arbitrage) 가능 → 탐지 필수!
| 분야 | 활용 |
|---|---|
| 금융 시스템 | 환율/가격 경로 분석, 불공정 거래 루프 탐지 |
| 네트워크 라우팅 | RIP(Route Information Protocol) 초기 버전 |
| 게임 개발 | 음수 이벤트(피해, 버프/디버프 포함한 이동 비용 등) |
| 교통/물류 | 특정 경로의 위험도, 지연 등 부정적 요소가 포함된 경로 계산 |
2. 알고리즘 개념의 기반이 됨
- Dynamic Programming 개념이 직관적으로 적용된 대표 사례
| 동적 프로그래밍 요소 | 벨만-포드에서의 적용 |
|---|---|
| 작은 문제로 나누기 | 간선 수 기준 거리 갱신 반복 |
| 하위 결과 재활용 | 이전 거리 값 사용 |
| 최적 부분 구조 | u까지의 최단 경로 + (u→v) = v까지 최단 경로 |
| 반복적 테이블 갱신 | 거리 배열(distance[]) 반복적으로 업데이트 |
| bottom-up 계산 | 간선 수 0 → 1 → ... → V-1로 증가하며 해 탐색 |
- Relaxation, 최적 부분 구조 등의 알고리즘적 사고 방식 학습에 유리
"이걸로 뭘 할 수 있는지"보다는
"이걸 통해 사고 구조를 어떻게 확장할 수 있는지"가 더 중요한 경우도 있어요.
3. 코딩 테스트 / 알고리즘 대회에 자주 출제
- 대놓고 “벨만-포드”라고 말하진 않지만, 음수 가중치 + 최단 거리 문제에서 자연스럽게 선택하게 되는 알고리즘
- 예시 유형:
- "최소 비용으로 이동" 문제인데 음의 비용 존재
- "음수 사이클이 존재하는지 판단하라"
- "일정 조건을 만족하는 루프가 가능한가?"
📝 백준 / 프로그래머스 등에서 대표 문제:
- 백준 11657 - 타임머신
- 백준 1219 - 오민식의 고민
- 백준 1865 - 웜홀 ← 음수 사이클 존재 여부
4. CS 기본기 + 인터뷰 대비
- 개발 면접이나 알고리즘 문제에서 면접관이 질문하기 딱 좋은 주제
- “다익스트라와 벨만-포드의 차이는?” → 단골 면접 질문
- 시스템, 네트워크 이론에서도 그래프와 경로 최적화 문제는 빈번히 등장**
'Develop > Coding Test | Algorithm' 카테고리의 다른 글
| 유니온-파인드 알고리즘 (2) | 2025.04.04 |
|---|---|
| 원형 큐 (0) | 2025.02.14 |
| Tree 전위, 중위, 후위 순회 (0) | 2024.11.07 |
| 알고리즘 정리 및 예제 (1) | 2024.10.22 |
| 기본 자료구조 및 사용법 정리 (0) | 2024.10.22 |


댓글